Problem Link
Polycarpus has a ribbon, its length is n. He wants to cut the ribbon in a way that fulfills the following two conditions:
Input
The first line contains four space-separated integers n, a, b and c (1 ≤ n, a, b, c ≤ 4000) — the length of the original ribbon and the acceptable lengths of the ribbon pieces after the cutting, correspondingly. The numbers a, b and c can coincide.
Output
Print a single number — the maximum possible number of ribbon pieces. It is guaranteed that at least one correct ribbon cutting exists.
Examples
input
In the first example, Polycarpus can cut the ribbon in such a way: the first piece has length 2, the second piece has length 3.
In the second example, Polycarpus can cut the ribbon in such a way: the first piece has length 5, the second piece has length 2.
Approach:
We are given a certain ribbon of length n and we are asked to cut the ribbon such that we have maximum pieces where each piece can be of length a, b, or c
Let f (n) be the function that gives the maximum number of pieces that a ribbon of length n be cut. Then,
so,
After, cutting the ribbon of length n we get a similar problem with reduced length(optimal substructure) and many repeating subproblems(try drawing recursion tree for the first test case). This is the characteristics of DP problems. So we can apply DP.
As top-down approach looks more natural let’s first implement this solution.
I’m going to use Python for this problem. The only problem with python is it has a recursion limit. So I’ve to explicitly set recursion limit to some maximum value.
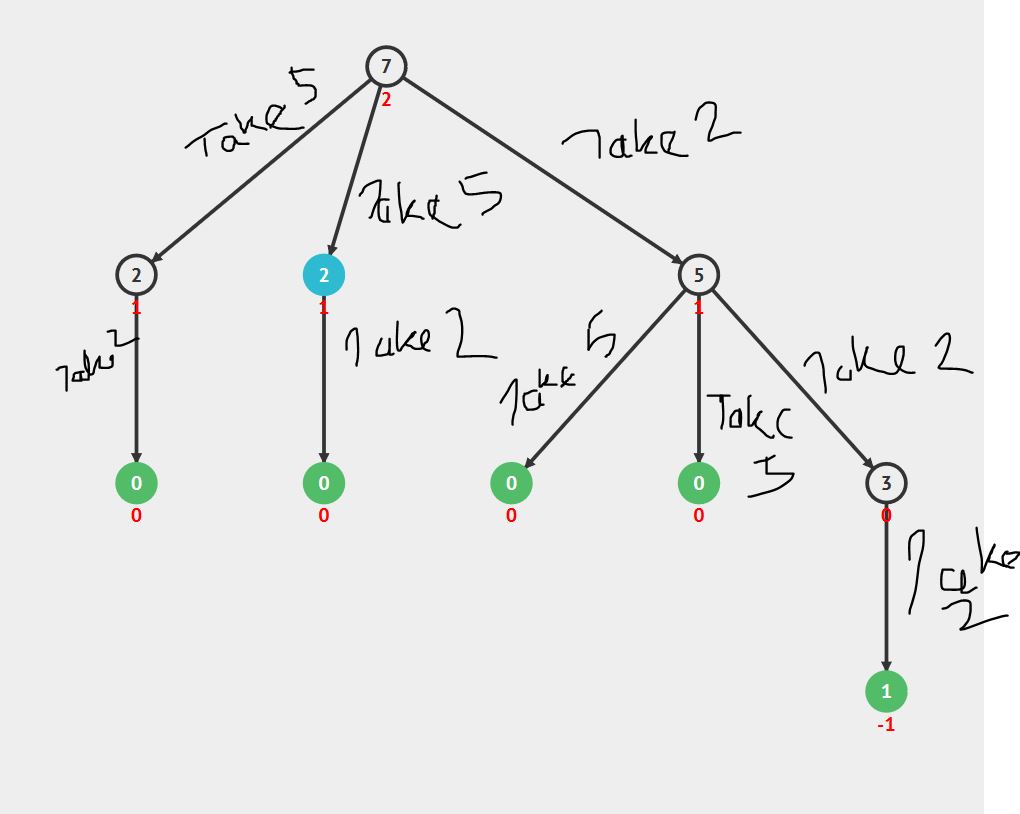
Let’s dive into our code
The solution for bottom of dp is just translating the above approach by building the solution for
Let
Initialize an array of length
Base case:
Polycarpus has a ribbon, its length is n. He wants to cut the ribbon in a way that fulfills the following two conditions:
- After the cutting, each ribbon piece should have length a, b or c.
- After cutting the number of ribbon pieces should be maximum.
Input
The first line contains four space-separated integers n, a, b and c (1 ≤ n, a, b, c ≤ 4000) — the length of the original ribbon and the acceptable lengths of the ribbon pieces after the cutting, correspondingly. The numbers a, b and c can coincide.
Output
Print a single number — the maximum possible number of ribbon pieces. It is guaranteed that at least one correct ribbon cutting exists.
Examples
input
5 5 3 2
2
7 5 5 2
2
In the first example, Polycarpus can cut the ribbon in such a way: the first piece has length 2, the second piece has length 3.
In the second example, Polycarpus can cut the ribbon in such a way: the first piece has length 5, the second piece has length 2.
Approach:
We are given a certain ribbon of length n and we are asked to cut the ribbon such that we have maximum pieces where each piece can be of length a, b, or c
Let f (n) be the function that gives the maximum number of pieces that a ribbon of length n be cut. Then,
f(n) = 1 + max(f(n - a),
f(n - b),
f(n - c))
so,
f(0) = 0After, cutting the ribbon of length n we get a similar problem with reduced length(optimal substructure) and many repeating subproblems(try drawing recursion tree for the first test case). This is the characteristics of DP problems. So we can apply DP.
As top-down approach looks more natural let’s first implement this solution.
I’m going to use Python for this problem. The only problem with python is it has a recursion limit. So I’ve to explicitly set recursion limit to some maximum value.
import sys
sys.setrecursionlimit(500000000)

Let’s dive into our code
#Author: Bishal Sarang
import sys
sys.setrecursionlimit(500000000)
def f(n):
"""
returns maximum number of pieces that can be cut for ribbon with length n
"""
# If maximum num of pieces for length n is already computed simply return it
if n in memo.keys():
return memo[n]
ans = float("-inf")
if n == 0:
return 0
for length in l:
# Cut into pieces if only we wont have negative length of ribbon
if n >= length:
ans = max(ans, 1 + f(n - length))
#Cache the result
memo[n] = ans
return ans
#Dict to store computed values
memo = dict()
# Read Input
l = list(map(int, input().split()))
n, l = l[0], l[1:]
print(f(n))
The solution for bottom of dp is just translating the above approach by building the solution for
length 1, length 2, length 3 ....upto length n.Let
dp[n] gives the maximum number of pieces possible for length n such that dp[i] gives the maximum number of pieces possible for length i where 1 <= i <= n.Initialize an array of length
(n + 1) with negative infinity denoting initially all length are not possible.Base case:
dp[0] = 0
dp[i] = max(dp[i],
1 + dp[i - a],
1 + dp[i - b],
1 + dp[i - c])
dp[i] in a more readable format using loop.for length in l:
# Cut into pieces if only we dont have negative length of ribbon
if i - length >= 0:
dp[i] = max(dp[i], 1 + dp[i - length])
#Author: Bishal Sarang
def f(n):
# Build maximum number of pieces for
#length 1 upto n in bottom up manner
dp = [float("-inf")] * (n + 1)
# Base Case
dp[0] = 0
# dp[i] gives maximum number of pieces that can
# be obtained by cutting ribbon of length i into pieces
# of length a, b or c
# dp[i] = -inf if it is not possible to cut the ribbon into pieces
for i in range(1, n + 1):
for length in l:
# Cut into pieces if only we dont have negative length of ribbon
if i - length >= 0:
dp[i] = max(dp[i], 1 + dp[i - length])
# return maximum number of pieces possible for ribbon with length n
return dp[n]
l = list(map(int, input().split()))
n, l = l[0], l[1:]
print(f(n))