Leetcode 78: Subsets

In this post, I'm going to talk about a problem on leetcode which asks us to find all the possible subsets of given list of integers. This problem is the base to solving other problems like subset sum and subset partitioning which I'll be discussing in coming posts. Let's get started: I'll be solving this problem using 2 techniques:

1. Using Recursion
2. Using Bitset

I'll be using cpp for this task.
Problem Statement: Given a set of distinct integers, nums, return all possible subsets (the power set).
Note: The solution set must not contain duplicate subsets.
Example: Input:

nums = [1,2,3]

Output:

[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

Solution

1. Using Recursion

Firstly, I'll be discussing recursive approach to subset finding problem. Recursive problem is easy to visualise. Consider the given testcase [1, 2, 3]. 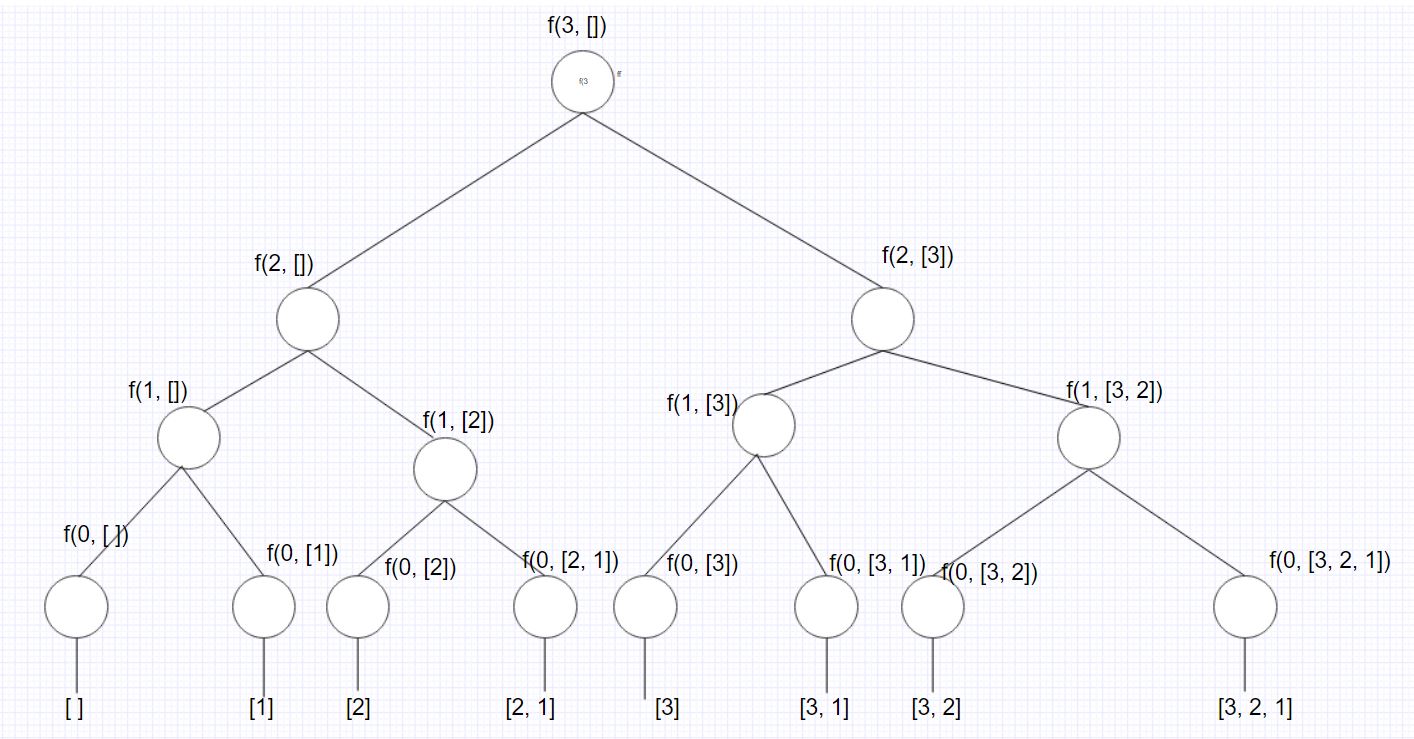Let solve(nums, n, subset) be the function that find subsets for array nums and number of elements n, initially called with an empty subset. So our initial call is :

vector<int>subset;
solve(nums, nums.size(), subset);

Now lets try visualising how recursion tree looks like.
Recursive Cases: For every state i.e (n), i,e position n - 1 of

solve(nums, n, subset)

we can have 2 choices:(Try to visualise recursion for arr = {1, 2, 3} )

• Don’t include the current element in the subset i.e simply call

solve(nums, n - 1, subset);

• Include current element in the subset
  

  subset.push_back(arr[n -  1]);
  solve(nums, n -  1, subset);
  

Base Cases:
Let’s think of base cases. The base cases are:

• If n == 0 i.e no item left push the current subset to our subsets_ which is a vector of vector.
  

  if (n == 0){
  subsets_.push_back(subset);
  return;
  }
  

  Complete Code:
  

  class Solution {
  public:
  // Vector of vector of int to store all the subsets
  vector<vector<int>> subsets_;
  
  // Solve method that generates subset recursively
  void solve(vector<int> &nums, int n, vector<int> subset){
      // If size of array becomes 0, no elemnts are left
      // We push current subset to our subsets_ and return
      if (n == 0){
          subsets_.push_back(subset);
          return;
      }
      // Else we have 2 options:
  
      // Don't include the current element to subset
      solve(nums, n - 1, subset);
      // Incldue the current element in subset
      subset.push_back(nums[n - 1]);
      solve(nums, n - 1, subset);
  }
  
  // Solution method subsets
  vector<vector<int>> subsets(vector<int>& nums) {
      // Make an empty vector subset
      vector<int> subset;
      // Call solve function initially with an empty subset 
      solve(nums, nums.size(), subset);
      // Return subsets after calculation
      return subsets_;
  }
  };
  

2. Using Bitset

I have explained the bitset method on quora.